课程内容提要

这里四种算法覆盖90%的考试情况,如果需要更多了解算法,建议学习下九大经典算法,难点在于后五大算法。可以看这个博主的热门文章:https://blog.csdn.net/qq_37763204/article/details/79289532
分治法

分而治之
分治法的“分”是将大问题拆分为子问题,然后再将子问题拆分为更小的子问题,以此类推;“治”则是由小而大递归地解决这些子问题。最后还需要“合”,就是将子问题的解合并,最终得出原问题的解。
分治法的思想非常朴素,是大学计算机系课程中肯定会讲到的内容,但它也是很多精妙算法的基础,比如排序算法中的归并排序和快速排序、计算几何中平面最近点对问题的解法、大整数乘法中的Karatsuba算法与Toom-Cook算法,以及快速傅里叶变换(FFT,也能解决大整数乘法)等。
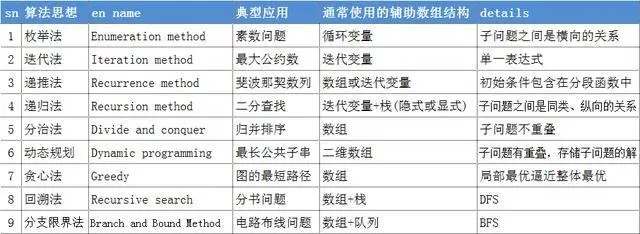
递归技术
上面的F(n)是一个斐波那契数列
案例:二分法查找

回溯法

回溯法思路的简单描述是:把问题的解空间转化成了图或者树的结构表示,然后使用深度优先搜索策略进行遍历,遍历的过程中记录和寻找所有可行解或者最优解。
经典问题
(1)装载问题
(2)0-1背包问题
(3)旅行售货员问题
(4)八皇后问题
(5)迷宫问题
(6)图的m着色问题摘自:https://blog.csdn.net/piyongduo3393/article/details/86003705
贪心算法
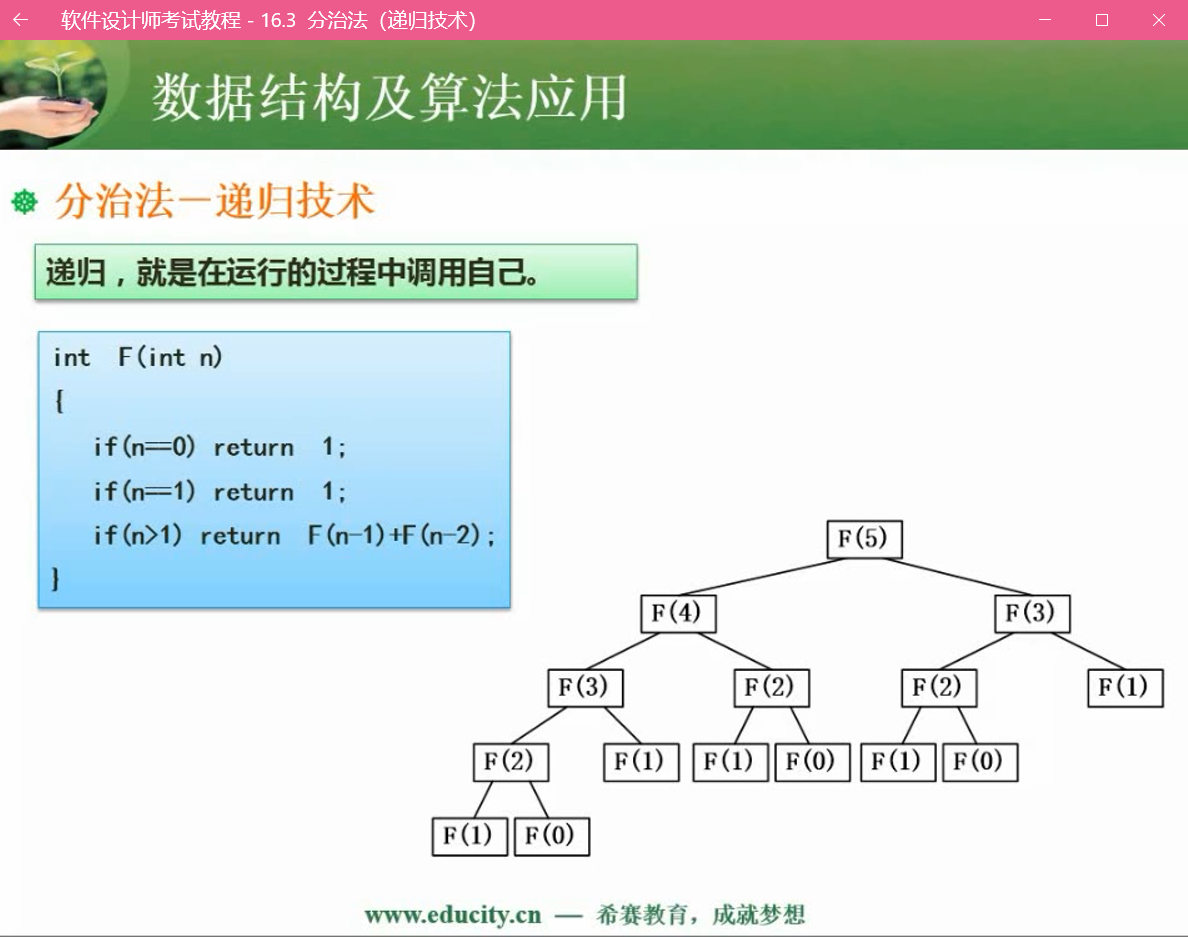
上面就是一个背包问题,有三个物品,怎么才能让背包装入最大的价值物品?
这里解题的思路是每次放入一个单位价值最高的物品到背包中。
这里得到的结果是b图的左边,总价值320,最优解是b图右边的380,如果物品不是三个而是三种,最优的解就是c图了。
贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解,但对范围相当广泛的许多问题他能产生整体最优解或者是整体最优解的近似解。
典型问题有:
背包问题
找零钱问题
活动安排问题
摘自:https://blog.csdn.net/qq_37763204/article/details/79289532
动态规划法
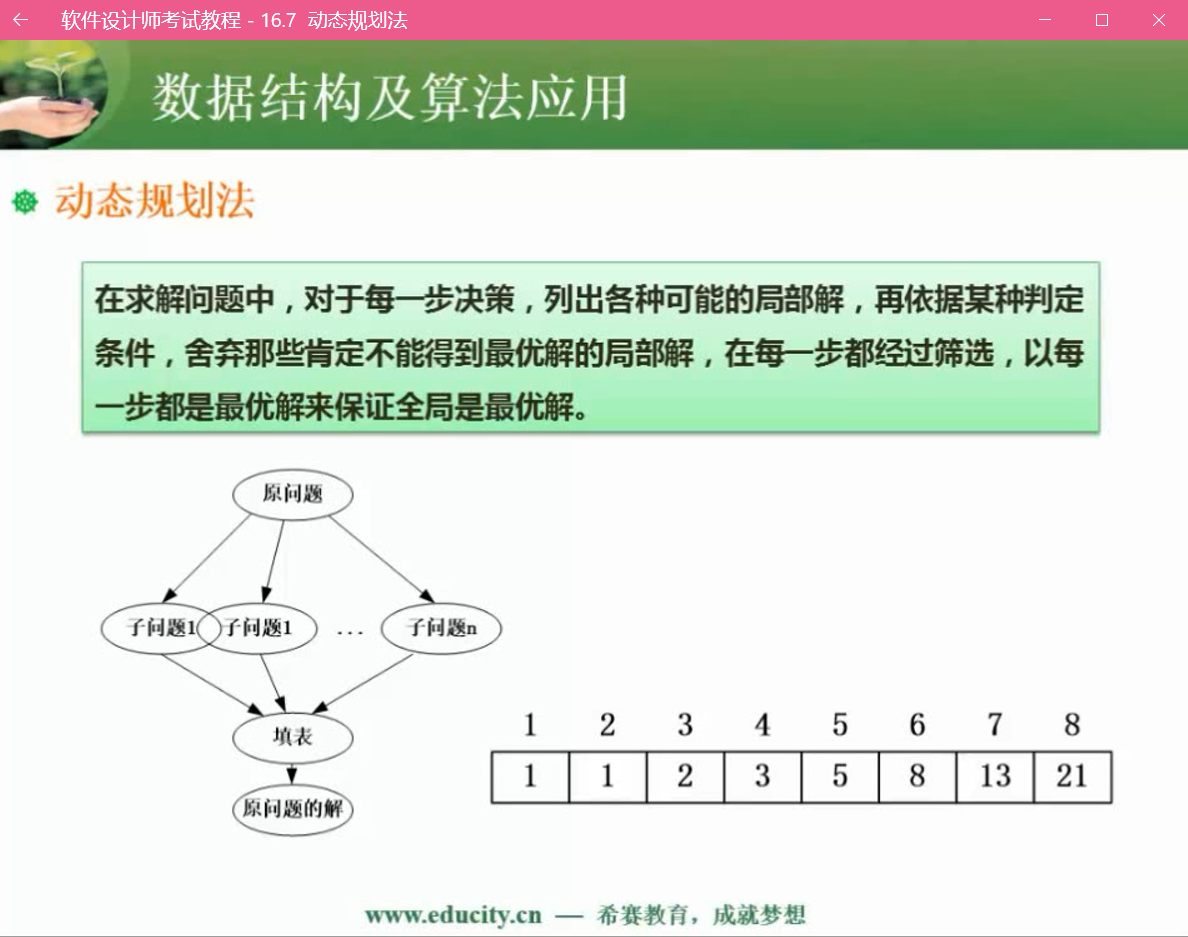
基本思想与分治法类似,也是将待求解的问题分解为若干个子问题(阶段),按顺序求解子阶段,前一子问题的解,为后一子问题的求解提供了实用的信息。
在求解任一子问题时,列出各种可能的局部解,通过决策保留那些有可能达到最优的局部解,丢弃其它局部解。依次解决各子问题,最后一个子问题就是初始问题的解。
因为动态规划解决的问题多数有重叠子问题这个特点。为降低反复计算。对每个子问题仅仅解一次,将其不同阶段的不同状态保存在一个二维数组中。
与分治法最大的区别是:适合于用动态规划法求解的问题,经分解后得到的子问题往往不是互相独立的(即下一个子阶段的求解是建立在上一个子阶段的解的基础上,进行进一步的求解)。
常见动态规划问题
找零钱问题
走方格问题
求最长公共序列数
摘自:https://blog.csdn.net/qq_37763204/article/details/79394397
试题1




问题1:
对于这个问题最好先完成第三题再来做会简单很多。
(1)j = 0
(2)b[j] += s[i]
(3)min = temp
(4)b[m] += s[i]
问题2:
贪心和贪心,O(n^2)和O(n^2)
因为两种策略都是追求局部最优,所以都是贪心算法
问题3:
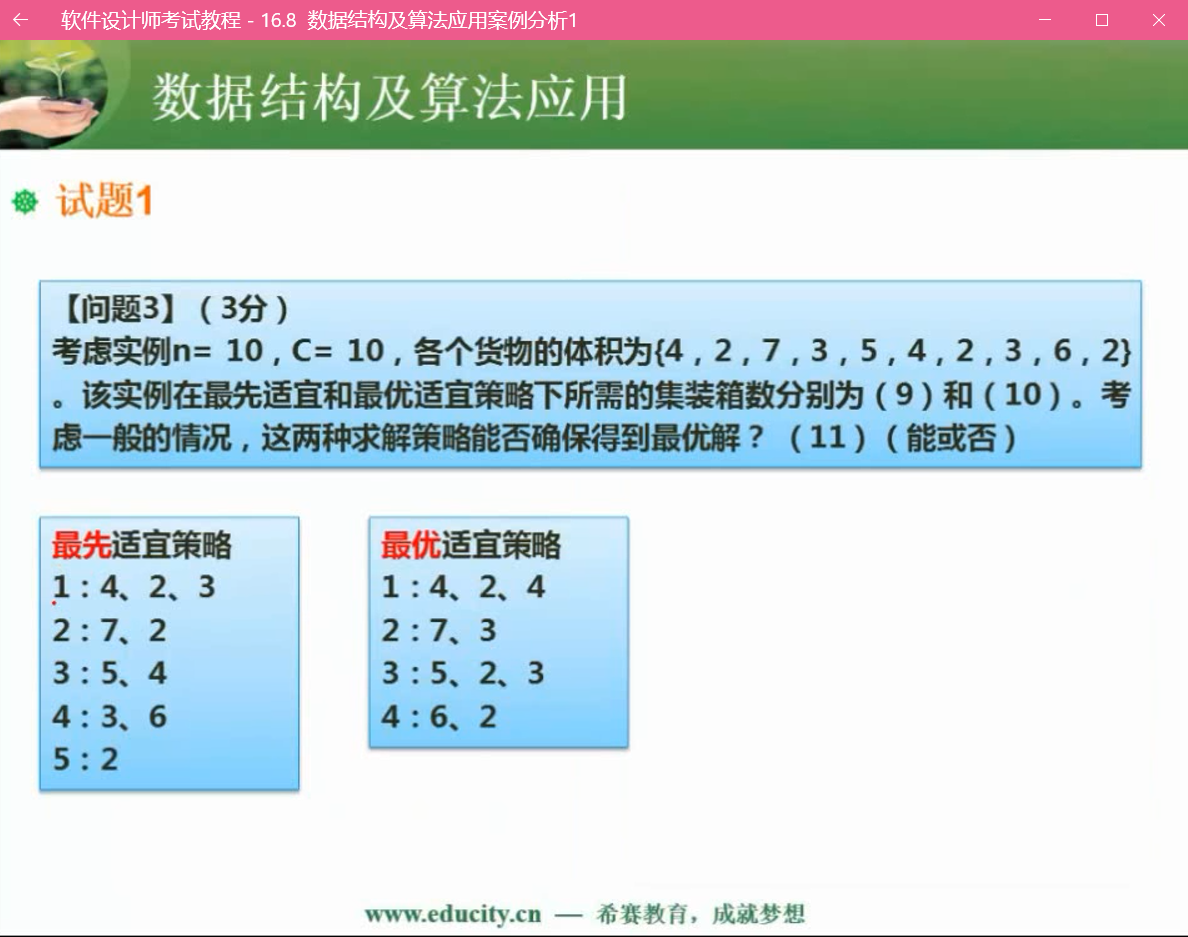
不能,这里最优适宜策略的解就比最先适宜策略更优,同时最优适宜策略是一种贪心算法,只能做到局部最优,无法做到整体最优。
试题2

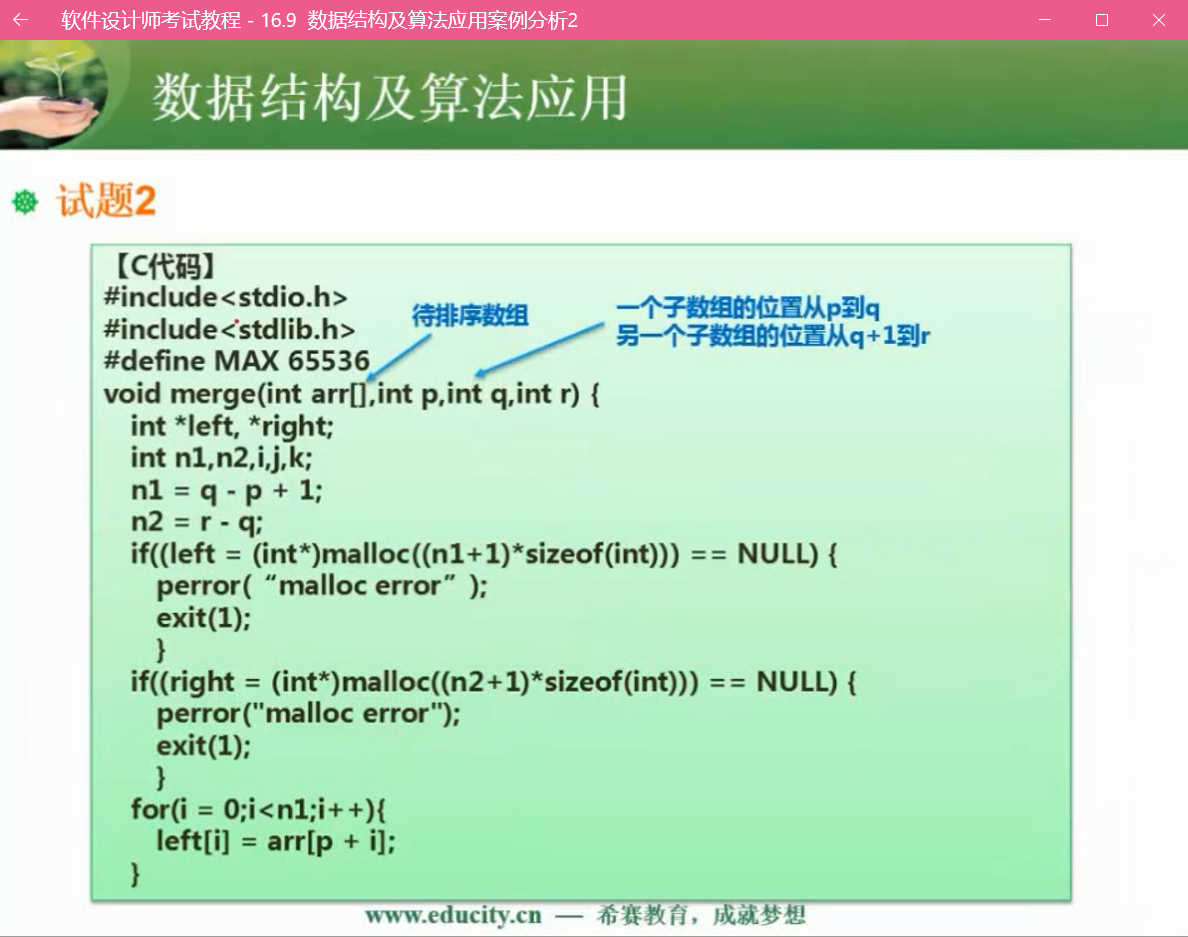

忽略红色部分的答案
问题1:
(1)k< = r
(2)arr[k] = right[j]
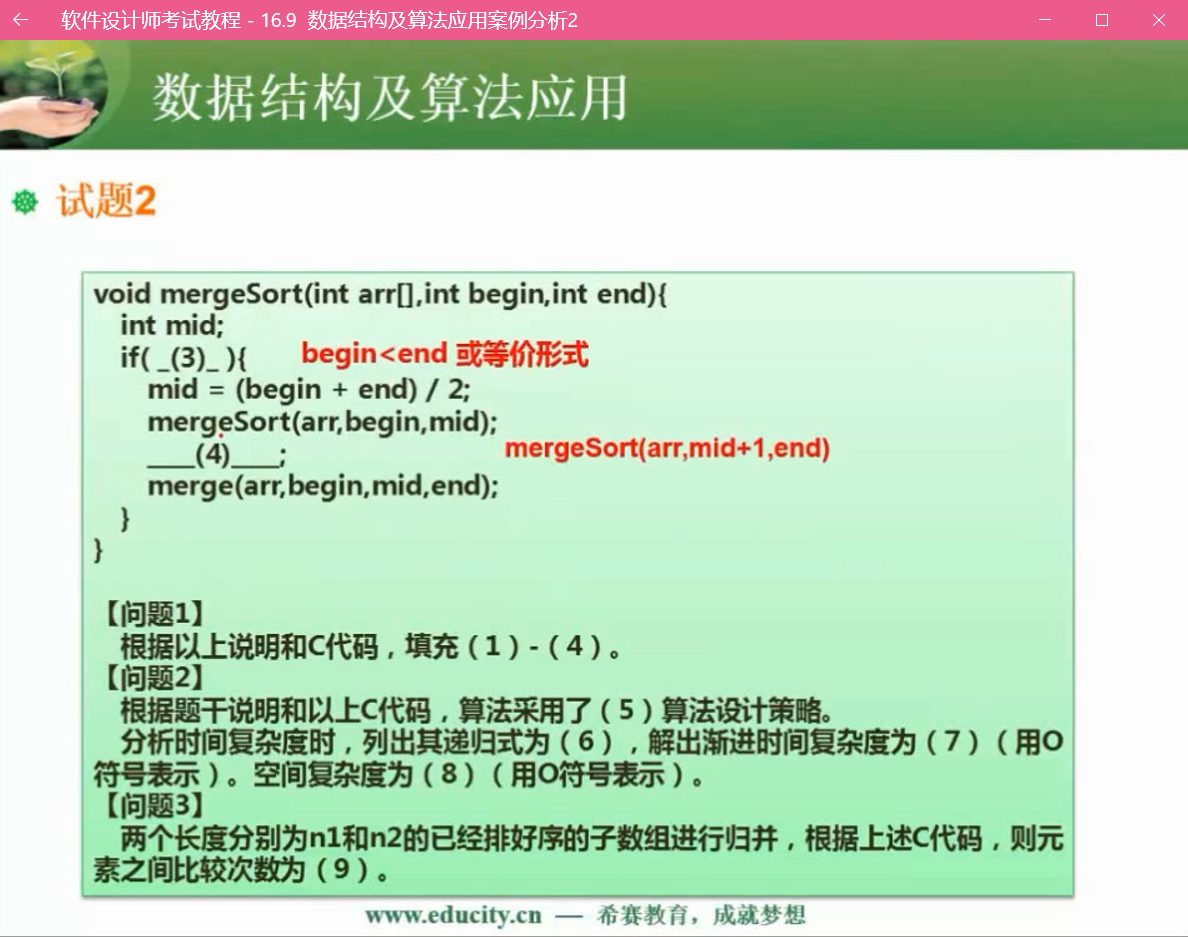
(3)begin < end
(4)mergeSort(arr, mid+1, end)
问题2:
分治, T(n) = 2T(n/2) +O(n), O(n*logn), O(n)
归并排序是分治法的典型应用。归并排序的时间复杂度为O(n*logn), 空间复杂度为O(n)
问题3:
n1+n2
本文链接: http://www.ionluo.cn/blog/posts/b6f479b8.html
版权声明: 本作品采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议 进行许可。转载请注明出处!
